組み合わせ C とは 公式や計算方法 は何通り 受験辞典
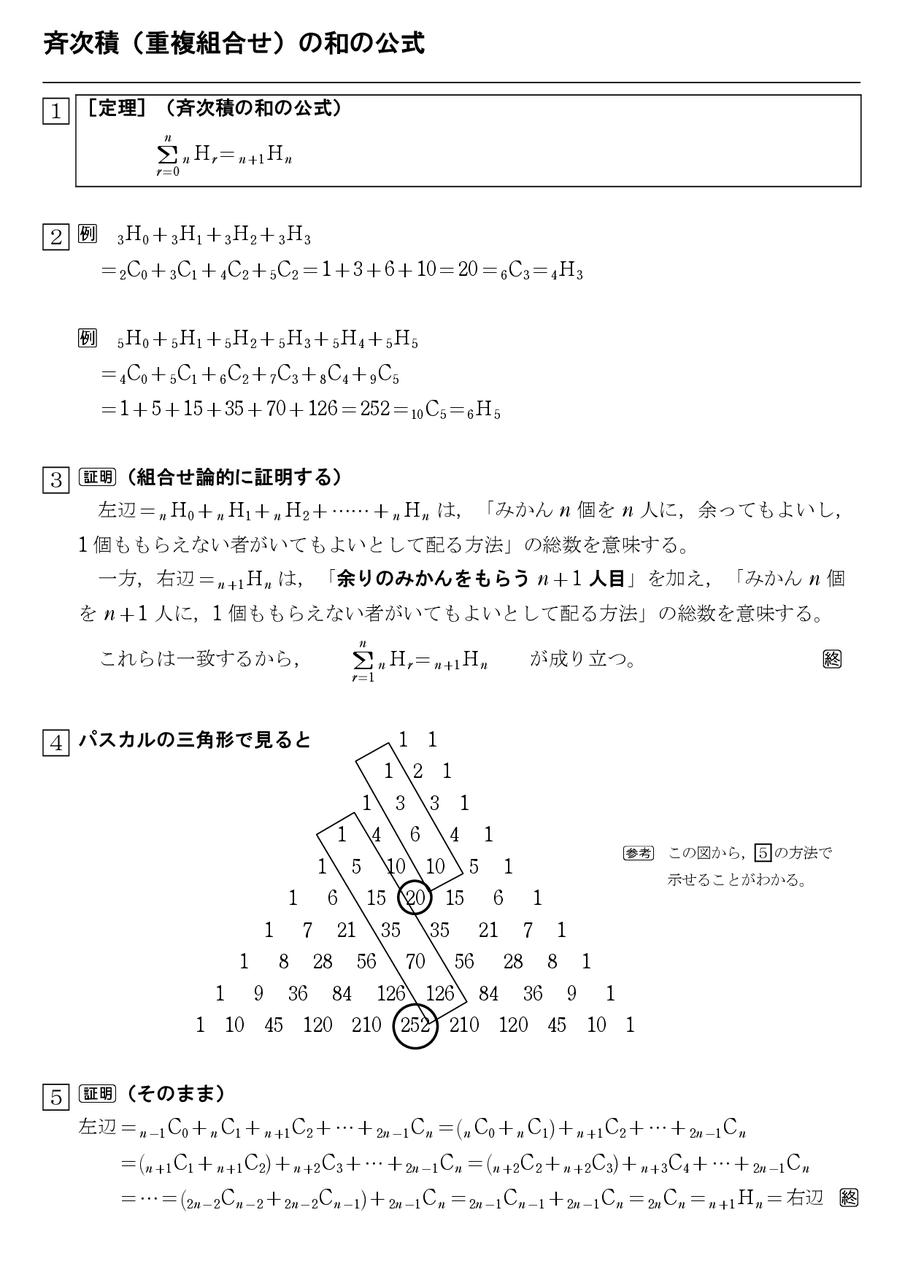
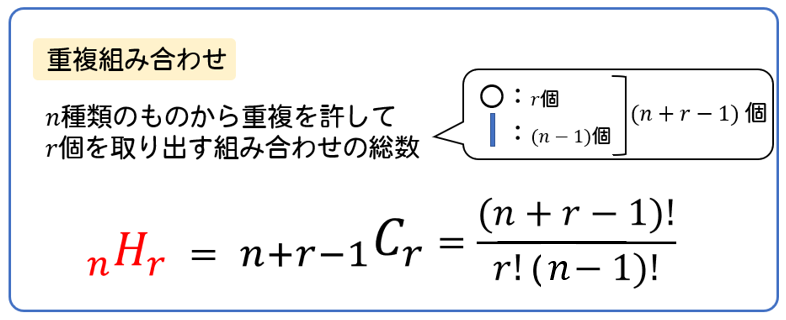
では, 重複組合せと対になるものは何だろうか 重複組合せの公式nHr は異なるn 個のものから重複を許してr 個選ぶときに使う この定義が難しい これも例をあげて考えてみよう 1,2,3 から重複をゆるして2 個選ぶなら, 11,12,13,22,23,33の6 通り その後でその区別をなくす。重複して数えている分を取り除く! この2つのプロセスで公式ができているため ! 公式の仕組みが同じなので 、同じものを含む順列の問題は組み合わせを使って解けます。 例えば、先ほどの3つのケーキを一列に並べる問題。
組み合わせ 公式 重複
組み合わせ 公式 重複-なお, n C r の C は「組み合わせ」という意味の"Combination"の頭文字"C"に由来します. さて,それでは n C r がどのように計算できるかを,次の問題を考えながら説明します. 1 から 4 までのいずれかの数字が書かれた4枚のカードがある.ただし,どの2そこで,重複順列から逆算して重複組合せを求めるという方針を推し進めても公式は得られません 2 具体例で考える ただ、重複順列 重複組み合わせの公式で、何故マイナス1なのか、文章からは、理解できません 理由を教えて頂ければうれしいです
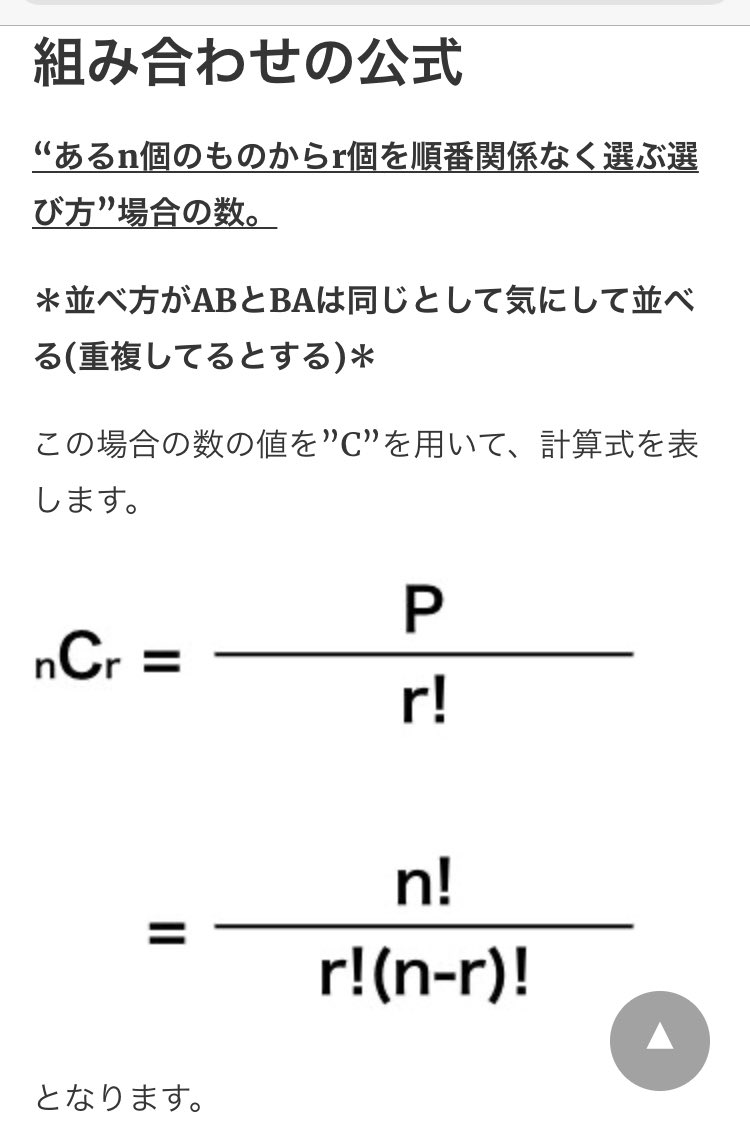
グラタン V Twitter Rt Komurazi Maki 式の計算はできるのですが なぜこの公式なのか というところが曖昧なので 英国紳士にはなれないです 昔から 計算はできるのに 正しい式を組み立てるのが苦手で T Co F2nmxefb0i Twitter
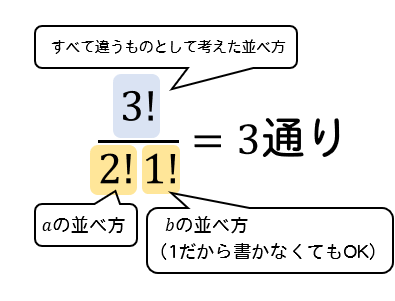
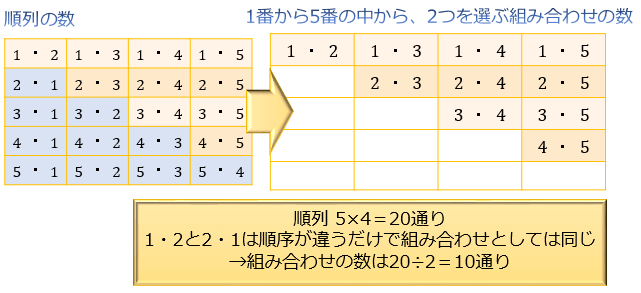
行く順番の組み合わせの数を求めよ。 答え:6通り。nPm(n=3,m=3を利用すればよい。)なお、nPn(n=3)は3の階乗と等しい。 組み合わせの公式 n個の異なるものからm個を抜き出した場合の組み合わせ数の公式は、以下のようになります。 利用例5分でサクッと解説! 組み合わせCの公式と使い方を徹底解説! 5分でサクッと解説! 今回はこんな悩みを解決します。 組み合わせのときはCを使うことは分かるけど、問題が解けません 「順列の公式と使い方」で順列の並び方について考えました 組み合わせの計算方法の証明 順列では、「並べる」という操作が入りますが、組み合わせでは「並べる」という操作は除外されます。 例えば、1, 2, 3の三つの数字について、順列の全ての場合を列挙すると次の6通りがあります。 組み合わせでは、上記6つ
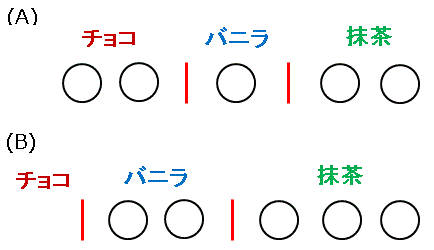
22 組み合わせの公式 組み合わせとは、「n 個の異なる要素の中から r 個を取り出す時の全事象の場合の数」のことです。順列との違いは、「並べ方が違っても要素が同じなら 1 通りである」と解釈する点です。 ここでは 通常の組み合わせ;= nm 1Cm = nHm 3 数列の積の総和 ∑n k=1 akbk = an ∑n k=1 bk ∑n k=1 (ak ak 1)k1 総和の公式集 ※何の断りも無ければ、m,n は自然数とします。 1m 次式の総和 ∑n k=1 k(k 1)(k 2)(k m 1) = n(n1)(n2)(nm) m1 または、 ∑n k=1 km 1Pm = nmPm1 m1 2m 重のシグマ ∑n a1=1 ∑a1 a2=1 ∑a2 a3=1 a∑m 1 am=1 1 = n(n1)(n2)(nm 1) m!
組み合わせ 公式 重複のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 |  | |
「組み合わせ 公式 重複」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「組み合わせ 公式 重複」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「組み合わせ 公式 重複」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
「組み合わせ 公式 重複」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「組み合わせ 公式 重複」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
「組み合わせ 公式 重複」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「組み合わせ 公式 重複」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「組み合わせ 公式 重複」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「組み合わせ 公式 重複」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「組み合わせ 公式 重複」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
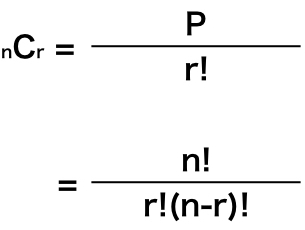 |  |  |
「組み合わせ 公式 重複」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
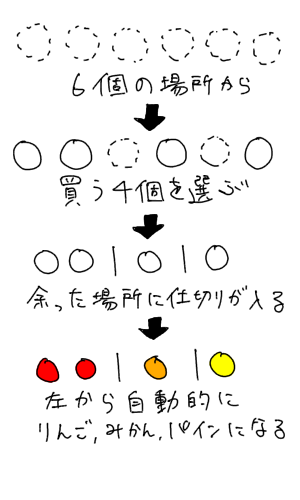
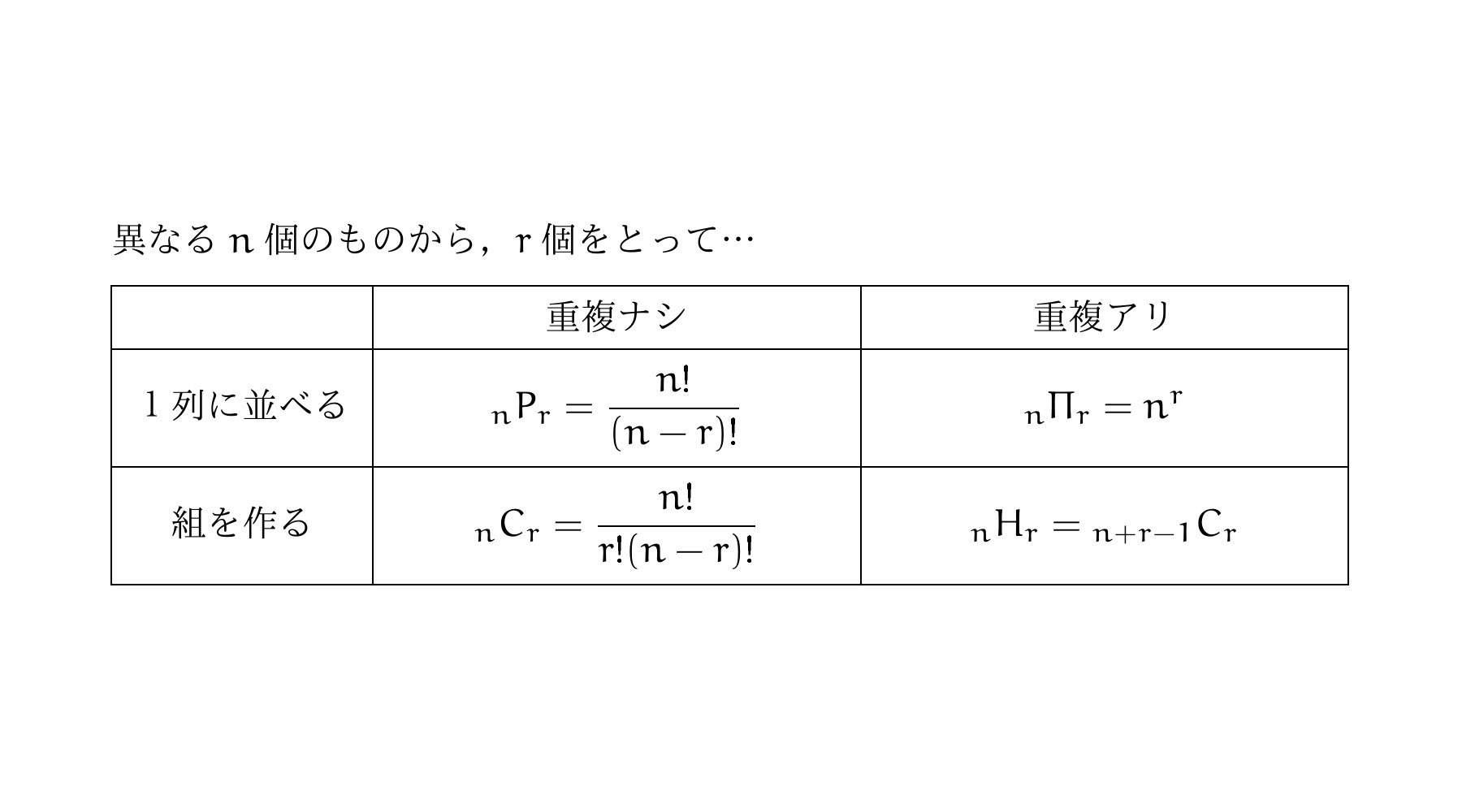
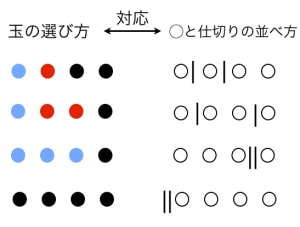
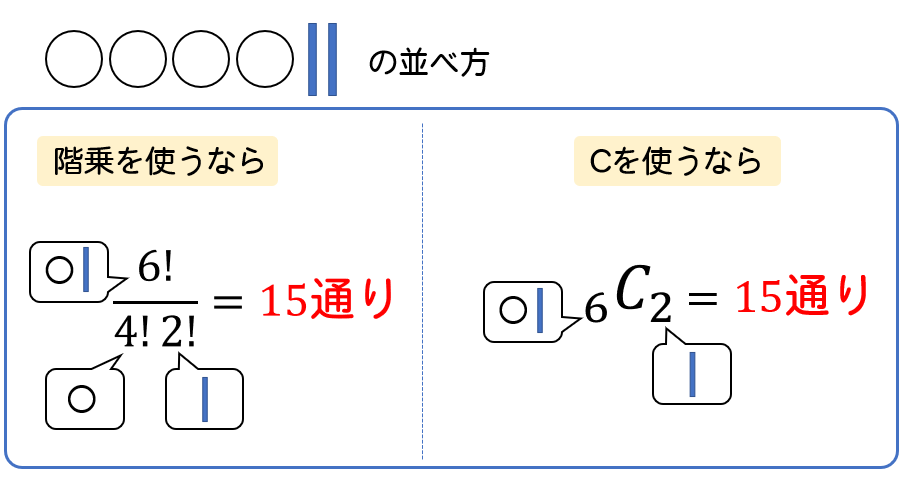
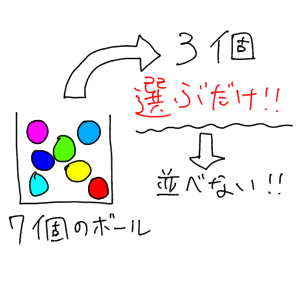
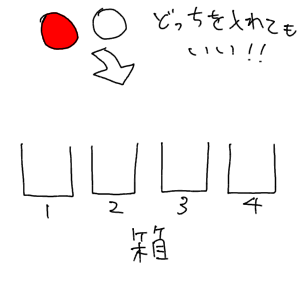
重複組合せの公式:nHrは今すぐ忘れるべし! 重複組合せの解法(例題1) 丸仕切り法とは (例題1−1)典型的な「区別が付かないものを区別がつくものに分ける」問題 2番は全員最低一個もらえるという部分が違うので少しだけ先に細工をしておきます 「どちらの公式を使うべきか少し迷った」という方も多いのではないでしょうか? このように、順列と組み合わせ、どちらの公式を使うべきか悩んだときに役に立つのが 「順番を並べかえたときに意味が変わるか?」 で考えるテクニックです。
Incoming Term: 組み合わせ 公式 重複, 組み合わせ 重複なし 公式,



